NL2HLTL2PLAN: Scaling Up Natural Language Understanding for Multi-Robots Through Hierarchical Temporal Logic Task Representation

Abstract

To enable non-experts to specify long-horizon, multi-robot collaborative tasks, language models are increasingly used to translate natural language commands into formal specifications. However, because translation can occur in multiple ways, such translations may lack accuracy or lead to inefficient multi-robot planning. Our key insight is that concise hierarchical specifications can simplify planning while remaining straightforward to derive from human instructions. We propose NL2HLTL2PLAN, a framework that translates natural language commands into hierarchical Linear Temporal Logic (LTL) and solves the corresponding planning problem. The translation involves two steps leveraging Large Language Models (LLMs). First, an LLM transforms instructions into a Hierarchical Task Tree, capturing logical and temporal relations. Next, a fine-tuned LLM converts sub-tasks into standard LTL formulas, which are aggregated into hierarchical specifications, with the lowest level corresponding to ordered robot actions. These specifications are then used with off-the-shelf planners. Our NL2HLTL2PLAN demonstrates the potential of LLMs in hierarchical reasoning for multi-robot task planning. Evaluations in simulation and real-world experiments with human participants show that NL2HLTL2PLAN outperforms existing methods, handling more complex instructions while achieving higher success rates and lower costs in task allocation and planning.

demo video

Overview

Overview of the framework, using the dishwasher loading problem as a case study. Note that the non-leaf nodes in the Hierarchical Task Tree (HTT), the language descriptions of sibling tasks, and the flat specifications are color-coded to indicate one-to-one correspondence.

The HTT tree is structured such that it unfolds level by level, where each child task is a decomposition of its parent task. Notably, the tasks at the bottom level are not necessarily indecomposable. This flexibility allows for varying numbers of levels and tasks per level, accommodating differences in task understanding and the range of primitive actions available to robot agents.

Additionally, it's important to highlight that the relation $R$ specifically captures the temporal relationships between sibling tasks that share the same parent. The temporal relationship between any two tasks in the tree can be inferred by tracing their lineage back to their common ancestor, thereby simplifying the overall complexity of the structure.

When a task instruction is received, we use LLMs to construct the HTT through a two-step process, as outlined in step 1.

Logical search: For every non-leaf node $v$, we gather its child tasks $V'$ and the temporal relations among them, defined by $R' \subseteq V' \times V'$. We then use LLMs to rephrase these child tasks and their temporal relations into syntactically correct sentences aligned with the semantics of LTL specifications (as illustrated in step 2.1). These reformulated sentences are input into a fine-tuned LLM that produces a single LTL formula (as depicted in step 2.2).
Action Completion: Given an HTT, each leaf node should represent a simple task on certain object, such as "task 1.1.1 place plates into the lower rack" in example. By viewing such simple task as a sequence of action steps, we prompt the LLM to generate a sequence of pre-defined API calls to expand the simple task. For instance, the symbol $\pi_{\text{plates}}^l$ that represents task 1.1.1 can be replaced with LTL specification composed of sequential APIs (step 2.2): $$\pi_{\text{plates}}^l = \Diamond ( \texttt{Pickup(plate)} \wedge \Diamond\, \texttt{Move(plate, lower_rack)})$$ After this step, a complete hierarchical LTL specifications is generated (example in step 2.1).

AI2-THOR experiments

To evaluate our method on tasks with more complex temporal requirements, we combine several base tasks in the The ALFRED dataset to generate derivative tasks (each derivative task can be composed with up to 4 base tasks).

We compare our method with SMART-LLM. SMART-LLM uses LLMs to generate Python scripts that invoke predefined APIs for the purposes of task decomposition and task allocation.

The metrics are as follows:

Success rate, which measures whether the target goal states of objects are achieved and if the order in which these states occur satisfies the specified temporal requirements.
Travel cost, measured in meters, is defined as the total distance traveled by all robots, excluding any costs related to manipulation.
Completion time, quantified as the number of discrete time steps required to complete the tasks.

1 base task with 4 robots: Place a computer on the ottoman

1 base task with 4 robots: Pick up a green candle and place it on the countertop

For derivatives tasks with 1 base task, our methods can effectively choose the shortest path while avoiding the repeating actions when executing sub-tasks, compared with the SMART-LLM which primarily seeks to identify a feasible solution without focusing on optimizing costs.

4 base tasks with 1 robot in dinning room

4 base tasks with 4 robots in dinning room

4 base tasks with 4 robots in bedroom

For derivative tasks with 4 base tasks, SMART-LLM failed to generate a feasible plan, as its prompt scripts always exceed the maximum content length the LLM accepts when the task content gradually becomes longer and more complex. However, as the HTT structure decomposes long tasks into tree-like dependencies, our method can effectively handle long tasks composed of multiple basic tasks, extract the temporal logic relationships, and provide planning. Here we demonstrated the planning of 4 robots under derivative tasks with 4 base tasks in two different environments.

Real-world experiments

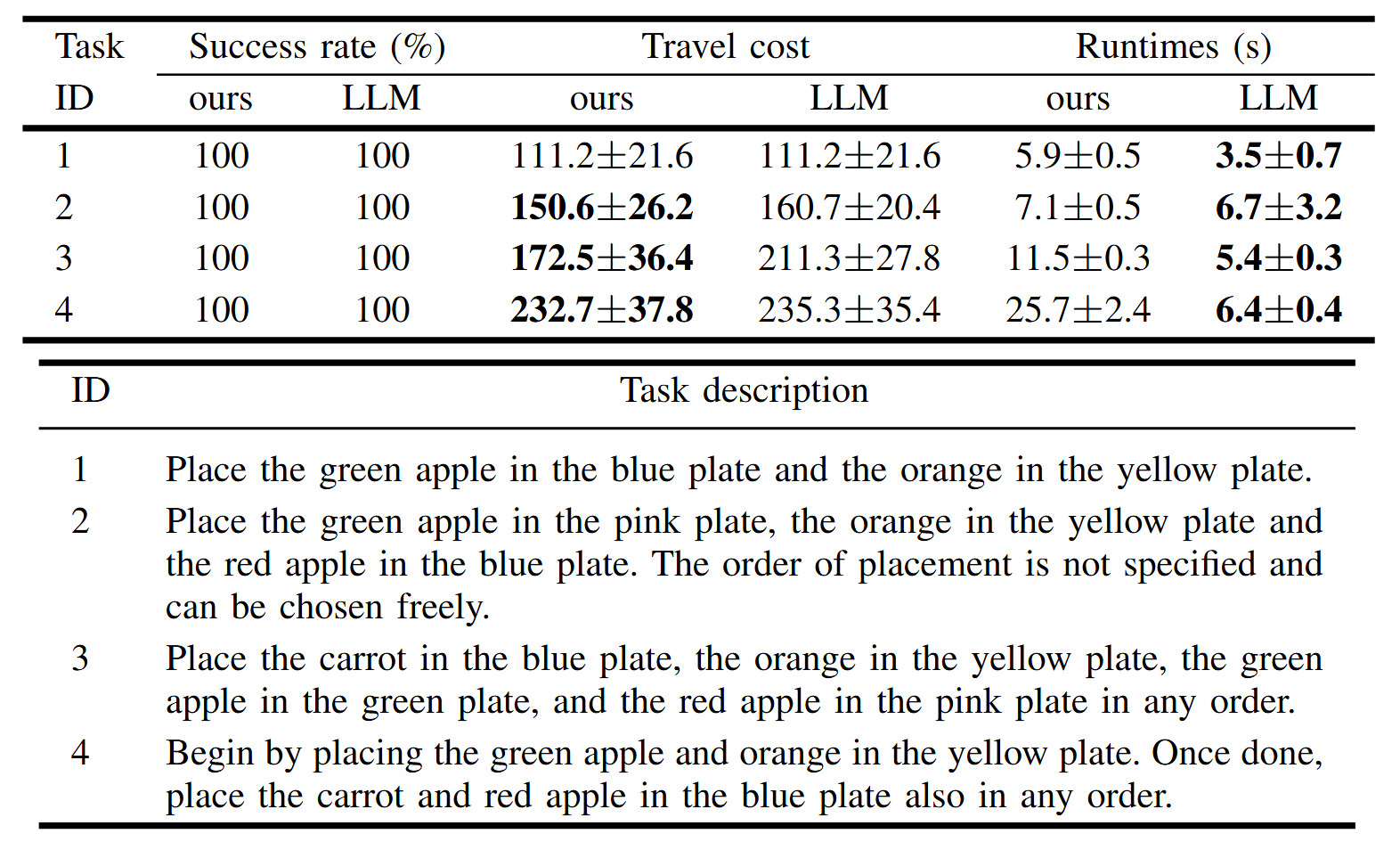
Our real-world experiments are conducted in a tabletop setting, where the task involves a robotic arm placing fruits and vegetables onto colored plates.

Given the primarily 2D nature of the task, we convert the tabletop environment into a discrete grid world. The use of only one robotic arm simplifies the task compared to the multi-robot scenarios in the simulator, as it eliminates the need for task allocation.

the adaptability to different verbal tones and styles from various users;
the comparative effectiveness of our plan solution against existing methods.

same task with different object arrangements

A sequence of images, arranged from left to right and top to bottom, depicts the task. "First, put a set of keychains on the armchair. Retrieve a pencil and put it on the side table. Move the phone and the bat to the bed in any order", objects and their trajectories are marked with different colors as follows, keychains (red), bat (blue), pencil (purple) and phone (green). $t$ represents the discrete time steps in simulation.

Snapshots depict four arms performing real-world tasks of picking and placing objects via handover. The instruction given is, "Please move the blue, green, and multi-colored blocks to the two opposite boxes, place the colored ones after the green ones."" Target areas are colored in magenta. The block being selected is emphasized with an ellipse, and the remaining blocks are contained within rectangles.

The figure above is a comparative overview of snapshots between our approach and LLMs for task "Place the green apple in the pink plate, the orange in the yellow plate and the red apple in the blue plate. The order of placement is not specified and can be chosen freely".

Our method gives an optimal plan based on the positions of the fruits, whereas LLMs basically follow the sequence in which the fruits are mentioned in the instructions.

As observed, both our approach and the LLM achieve a high success rate, which aligns with the expectations given the task complexities. This confirms that our method is capable of adapting to various user instructions. Regarding cost, for the first four tasks that require sequential actions, the costs are identical. For the latter four tasks, which allow for multiple feasible solutions, our method consistently produces lower-cost paths, with the exception of task 5. In this simple task, the LLM also manages to create an optimal plan based on the placement of fruits.

Prompts

Conversion from human instructions to Hierarchical Task Tree:
Prompt for generating HTT task decomposition | Prompt for extracting relationships between HTT sibling tasks

Generation of task-wise flat LTL specifications:
Nature language to LTL formula via a finetuned LLM | Prompt for action completion | An example of generated hierarchical LTL specifications

Prompts for real-world experiments:
Prompt for LLMs to generate task plan | Prompt for LLMs to generate task plan for multi-robot handover task

Instructions for Real-world Experiments

A collection of representative tasks along with their rephrasings
Task description for multi-robot handover experiments

Instructions for AI2-THOR Experiments

A list of these derivative tasks with 4 base tasks
A collection of derivative tasks composed of 1-4 base tasks